विषयसूची:
- चरण 1: समान वर्गों का एक NxN मैट्रिक्स उत्पन्न करें
- चरण 2: नेटवर्क को यादृच्छिक बनाना
- चरण 3: नई दूरियां प्राप्त करें
- चरण 4: एक बिंदु का चयन करें और उस बिंदु से दूसरे की दूरी की तुलना करें
- चरण 5: एक नए बिंदु पर जाएँ
- चरण 6: बल = K*दूरी
- चरण 7: स्थानांतरित बिंदु के कारण नेटवर्क आंदोलन बदलें
- चरण 8: समाप्त कोड

वीडियो: बाहरी बल के साथ विस्थापित होने पर उत्पन्न फाइबर नेटवर्क के बल परिवर्तन को मापना: 8 कदम

2024 लेखक: John Day | [email protected]. अंतिम बार संशोधित: 2024-01-30 09:22

कोशिकाएं अपने आस-पास के बाह्य मैट्रिक्स (ईसीएम) के साथ बातचीत करने में सक्षम हैं और दोनों ईसीएम द्वारा लगाए गए बलों पर लागू होने के साथ-साथ प्रतिक्रिया भी कर सकती हैं। हमारी परियोजना के लिए, हम फाइबर के एक इंटरलिंक्ड नेटवर्क का अनुकरण करते हैं जो ईसीएम के रूप में कार्य करेगा और देखें कि नेटवर्क किसी एक बिंदु के आंदोलन के जवाब में कैसे बदलता है। ईसीएम को स्प्रिंग्स की एक इंटरलिंक्ड सिस्टम के रूप में तैयार किया गया है जो शुरू में शून्य के शुद्ध बल के साथ संतुलन में हैं। चूंकि बिंदु आंदोलन के जवाब में नेटवर्क पर बल लागू होता है, हम बल पर प्रतिक्रिया करने के लिए जुड़े बिंदुओं को इस तरह से प्राप्त करने का प्रयास करते हैं कि वे संतुलन में लौटने का प्रयास करते हैं। बल की निगरानी समीकरण F=k*x द्वारा की जाती है जहां k वसंत स्थिरांक है और x फाइबर लंबाई में परिवर्तन है। यह अनुकरण रेशेदार नेटवर्क में बल प्रसार की एक सामान्य समझ देने में मदद कर सकता है जिसका उपयोग अंततः मैकेनोट्रांसडक्शन को अनुकरण करने में मदद के लिए किया जा सकता है।
चरण 1: समान वर्गों का एक NxN मैट्रिक्स उत्पन्न करें


कोड शुरू करने के लिए, हम N चुनते हैं जो हमारे नेटवर्क (NxN) के आयामों को निर्धारित करेगा। आवश्यकतानुसार नेटवर्क आयामों को बदलने के लिए N के मान को मैन्युअल रूप से बदला जा सकता है। इस उदाहरण में, N=8 इसलिए हमारे पास पॉइंट्स का 8x8 नेटवर्क है। मैट्रिक्स उत्पन्न करने के बाद, हम मैट्रिक्स में सभी बिंदुओं को जोड़ते हैं जिनकी लंबाई 1 इकाई है, दूरी सूत्र का उपयोग करके, दूरी = वर्ग ((x2-x1) ^ 2 + (y2-y1) ^ 2)। ऐसा करने से, हमें वर्गों का एक नेटवर्क मिलता है जो सभी समान रूप से 1 इकाई से बाहर होते हैं। इसे चित्र 101 में देखा जा सकता है।
चरण 2: नेटवर्क को यादृच्छिक बनाना


इस चरण में, हम बाहरी बिंदुओं को छोड़कर सभी बिंदु स्थानों को यादृच्छिक बनाना चाहते हैं जो हमारी सीमा बनाएंगे। ऐसा करने के लिए, हम पहले सभी मैट्रिक्स निर्देशांक ढूंढते हैं जो 0 या एन के बराबर होते हैं। ये बिंदु वे हैं जो सीमा बनाते हैं। गैर-सीमा बिंदुओं के लिए, x और y दोनों स्थितियों में -5 से.5 तक भिन्न यादृच्छिक मान जोड़कर स्थान को यादृच्छिक बनाया जाता है। प्लॉट की गई यादृच्छिक छवि को चित्र 1में देखा जा सकता है।
चरण 3: नई दूरियां प्राप्त करें

एक बार हमारा रैंडमाइज्ड नेटवर्क बन जाने के बाद, हम फिर से डिस्टेंस फॉर्मूला का उपयोग करके कनेक्टेड पॉइंट्स के बीच की दूरी का पता लगाते हैं।
चरण 4: एक बिंदु का चयन करें और उस बिंदु से दूसरे की दूरी की तुलना करें



इस चरण में, हम कर्सर का उपयोग करके रुचि के बिंदु का चयन कर सकते हैं, जैसा कि चित्र 2 में दिखाया गया है। आपको अपने कर्सर को बिल्कुल बिंदु पर ले जाने की आवश्यकता नहीं है क्योंकि कोड इसे निकटतम कनेक्शन बिंदु पर समायोजित कर देगा। ऐसा करने के लिए, हम पहले सभी जुड़े हुए बिंदुओं और हमारे द्वारा चुने गए बिंदु के बीच की दूरी की गणना करते हैं। सभी दूरियों की गणना के बाद, हम वास्तविक चयनित बिंदु बनने के लिए चयनित बिंदु से सबसे छोटी दूरी वाले बिंदु का चयन करते हैं।
चरण 5: एक नए बिंदु पर जाएँ



इस चरण में, पिछले चरण में चुने गए बिंदु का उपयोग करके, हम बिंदु को एक नए स्थान पर ले जाते हैं। यह आंदोलन कर्सर के साथ एक नई स्थिति का चयन करके किया जाता है जो पिछली स्थिति को बदल देगा। इस आंदोलन का उपयोग वसंत की लंबाई में परिवर्तन के कारण एक बाहरी बल का अनुकरण करने के लिए किया जाएगा। ऑल ब्लू फिगर में एक नए स्थान का चयन किया जा रहा है। अगले आंकड़े में, आंदोलन को नारंगी कनेक्शनों के साथ देखा जा सकता है जो पुराने स्थान थे जो नीले कनेक्शन के विपरीत नए स्थान हैं।
चरण 6: बल = K*दूरी

इस चरण में हम समीकरण बल = k * दूरी लागू करते हैं, जहां k कोलेजन फाइबर के लिए एक स्थिर 10 है। क्योंकि फाइबर नेटवर्क अपनी संतुलन स्थिति से शुरू होता है, शुद्ध बल 0 होता है। हम इस संतुलन का प्रतिनिधित्व करने के लिए पहले उत्पन्न मैट्रिक्स की लंबाई शून्य वेक्टर बनाते हैं।
चरण 7: स्थानांतरित बिंदु के कारण नेटवर्क आंदोलन बदलें




इस चरण में, हम बिंदु आंदोलन के जवाब में नेटवर्क की गति का अनुकरण करते हैं ताकि उसकी संतुलन स्थिति में वापस आ सकें। हम दो बिंदुओं के बीच नई दूरियों को खोजने से शुरू करते हैं। इससे हम पुरानी और नई दूरियों के बीच के अंतर को देखकर फाइबर की लंबाई में बदलाव का पता लगा सकते हैं। हम नए और पुराने बिंदु स्थानों की तुलना करके यह भी देख सकते हैं कि कौन से बिंदु चले गए हैं और वे बिंदु भी जिनसे वे जुड़े हुए हैं। यह हमें यह देखने की अनुमति देता है कि लगाए गए बल के जवाब में किन बिंदुओं को आगे बढ़ना चाहिए। आंदोलन की दिशा को इसके x और y घटकों में विभाजित किया जा सकता है, जिससे 2D दिशा वेक्टर मिलता है। k मान, दूरी में परिवर्तन और दिशा वेक्टर का उपयोग करके, हम बल वेक्टर की गणना कर सकते हैं जिसका उपयोग हमारे बिंदुओं को संतुलन की ओर ले जाने के लिए किया जा सकता है। हम कोड के इस खंड को 100 बार चलाते हैं, हर बार Force*.1 की वृद्धि में आगे बढ़ते हुए। कोड को 100 बार चलाने से हम अंततः फिर से संतुलन तक पहुँच सकते हैं और सीमा की स्थिति को ध्यान में रखते हुए हम केवल एक संपूर्ण बदलाव के बजाय नेटवर्क में बदलाव देखते हैं। नेटवर्क आंदोलन को चित्र 3 में देखा जा सकता है जिसमें पीला स्थानांतरित स्थान है और नीला पिछली स्थिति है।
चरण 8: समाप्त कोड
इस खंड में संलग्न हमारे कोड की एक प्रति है। विभिन्न नेटवर्कों के मॉडलिंग के साथ अपनी आवश्यकताओं के अनुरूप इसे संशोधित करने के लिए स्वतंत्र महसूस करें!
सिफारिश की:
पायथन में जलवायु परिवर्तन से तापमान परिवर्तन का रेखांकन: 6 कदम
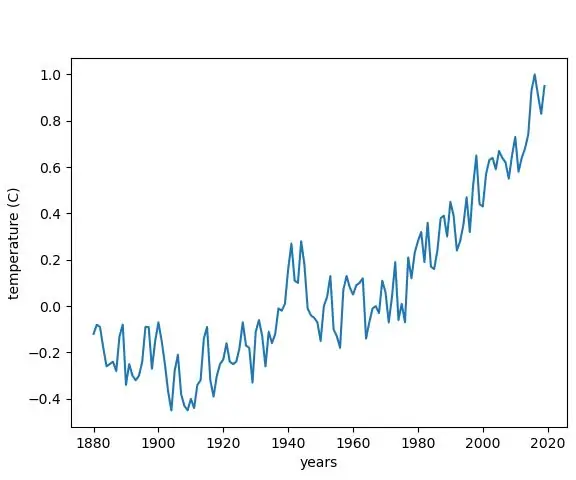
पायथन में जलवायु परिवर्तन से तापमान परिवर्तन का ग्राफिंग: जलवायु परिवर्तन एक बड़ी समस्या है। और बहुत से लोग अब नहीं जानते कि यह कितना बढ़ गया है। इस निर्देश में, हम जलवायु परिवर्तन के कारण जलवायु में तापमान परिवर्तन का रेखांकन करेंगे। चीट शीट के लिए, आप नीचे दिए गए पायथन फ़ाइल को देख सकते हैं
कार्बन फाइबर डेक के साथ पागल इलेक्ट्रिक लॉन्गबोर्ड बजट: 6 कदम (चित्रों के साथ)

कार्बन फाइबर डेक के साथ पागल इलेक्ट्रिक लॉन्गबोर्ड बुडेट: इससे पहले कि मैं अपने बारे में बात करूं और मैंने इस यात्रा पर जाने का फैसला क्यों किया, मैं यह कहना चाहूंगा कि कृपया एक महाकाव्य सवारी असेंबल के लिए मेरा vid देखें और मेरी बनाने की प्रथाओं को भी महत्वपूर्ण रूप से सदस्यता लें। वास्तव में मेरे कॉलेज के पाठ्यक्रम में मदद करेगा, क्योंकि
एर्गोमीटर बाइक के साथ वोल्टेज उत्पन्न करना: 9 कदम (चित्रों के साथ)

एक एर्गोमीटर बाइक के साथ वोल्टेज उत्पन्न करना: परियोजना के विस्तार में एक "गेम" की असेंबली शामिल थी, जिसका उद्देश्य जनरेटर से जुड़ी एर्गोमीटर बाइक में पेडल करना और इंजन की गति बढ़ने पर सक्रिय होने वाले लैंप के टॉवर को शामिल करना था - जो कि इसके अनुसार होता है साइकिल
पुरानी बाहरी सीडी/आरडब्ल्यू से एक बाहरी एचडीडी बनाएं: 5 कदम

पुरानी बाहरी सीडी/आरडब्ल्यू से एक बाहरी एचडीडी बनाएं: एक पुराने बाहरी सीडी/आरडब्ल्यू का एक अधिक उपयोगी बाहरी हार्ड ड्राइव में सीधे रूपांतरण। आपूर्ति 1-बाहरी सीडी/आरडब्ल्यू (अधिमानतः अधिक बॉक्सी प्रकार) 1-हार्ड ड्राइव (ड्राइव केस के आंतरिक कनेक्टर से मेल खाना चाहिए, स्वरूपित/sysed होना चाहिए) 1-एसएम
अपने वायरलेस नेटवर्क राउटर को कैसे ठंडा करें और इसे धीमा होने से कैसे रोकें: 3 कदम

अपने वायरलेस नेटवर्क राउटर को कैसे ठंडा करें और इसे धीमा होने से कैसे रोकें: यह एक निर्देश योग्य है जो आपको दिखाता है कि आप अपने वायरलेस नेटवर्क राउटर को कैसे ठंडा करें और धीमा होने से बचें। मैंने वायरलेस को ठंडा करने के लिए कंप्यूटर के पंखे का उपयोग किया, पंखे को वायरलेस से जोड़ा और उपयोग करेगा वायरलेस का एक ही पावर स्रोत (वायरलेस नो फैन ऑन, वाई
