विषयसूची:
- आपूर्ति
- चरण 1: पेंडुलम क्या हैं? इसे कैसे मॉडल करें?
- चरण 2: हार्डवेयर बिल्डिंग के लिए पुर्जे तैयार करें
- चरण 3: प्रयोग डेटा संग्रह
- चरण 4: डेटा विश्लेषण
- चरण 5: भविष्य के कार्य अनुशंसाएँ

वीडियो: सरल हार्मोनिक गति का प्रायोगिक अध्ययन: 5 कदम

2024 लेखक: John Day | [email protected]. अंतिम बार संशोधित: 2024-01-30 09:20
लेखक द्वारा और अधिक का पालन करें:


कक्षा में, हम अक्सर पेंडुलम प्रयोग, या सरल हार्मोनिक गति प्रयोग करने के लिए स्टॉपवॉच का उपयोग करते हैं। यहां एक चुनौती है, क्या हम इसके आंदोलन का वास्तविक ग्राफ तैयार कर सकते हैं और देख सकते हैं कि तात्कालिक कोणीय स्थिति और वेग क्या है, यह बहुत अधिक जानकारी और मजेदार है।
पहला प्रश्न, हमें यह तय करने की आवश्यकता है कि पेंडुलम शरीर एक भारहीन कॉर्ड या एक कठोर वर्दी रॉड है। कॉर्ड दृष्टिकोण आसान लगता है। एक के निर्माण के अभ्यास से, मेरे पास निम्नलिखित ट्रेडऑफ़ विचार हैं: पेंडुलम सिस्टम को लटकाने का सबसे आसान तरीका यह हो सकता है कि इसे आपके दरवाजे के ऊपरी किनारे पर लटका दिया जाए। यह बिना किसी संरचनात्मक निर्माण कार्य के आपकी ~ 2m पेंडुलम लंबाई देता है। लेकिन इसके लिए जरूरी है कि झूला दरवाजे की सतह को न छुए, जो पूरे प्रयोग को बर्बाद कर देता है। तो जिस विमान से यह झूलता है वह आपकी दीवार/दरवाजे की सतह के बिल्कुल समानांतर होना चाहिए। एक भारहीन रस्सी पतली होती है, यह आसानी से घूम सकती है, और स्विंग कोण के माप को जटिल बना सकती है। हम स्विंग राज्य का प्रतिनिधित्व करने के लिए एक माप का उपयोग करना चाहते हैं। पतली रस्सी, जैसे कि मछली की रेखा, लोचदार और फैली हुई हो सकती है, जो हमारे द्वारा मापी गई और समीकरण में उपयोग की जाने वाली हमारे सबसे महत्वपूर्ण स्थिरांकों में से एक को प्रभावित करती है, जो पेंडुलम की लंबाई है। कुछ तापमान से भी प्रभावित हो सकते हैं। कॉर्ड के अंत में लटका हुआ भार द्रव्यमान इतना भारी होना चाहिए कि कॉर्ड का वजन नगण्य हो जाए। कृपया टिप्पणी करें कि क्या आप उनसे सहमत या असहमत हैं, या आपके पास अन्य डिज़ाइन ट्रेडऑफ़ विचार हैं। इस समस्या का अध्ययन करने के लिए, हमें एक ऐसे उपकरण की आवश्यकता है जो इतना हल्का हो कि उसके वजन को नजरअंदाज किया जा सके और हम अभी भी पेंडुलम प्रणाली को एक कठोर वर्दी रॉड के रूप में मानते हैं। मैं एक सीओटीएस पहनने योग्य इलेक्ट्रॉनिक नियंत्रक का उपयोग कर रहा हूं, जो ब्लूटूथ कनेक्शन के माध्यम से हमें जीरो, एक्सेलेरोमीटर और कोण की जानकारी प्रदान करता है। इन मापों को मोबाइल फ़ोन ऐप डेटा फ़ाइल में संग्रहीत किया जाएगा। उसके बाद, हम अपने सरल हार्मोनिक गति प्रयोग के लिए डेटा का विश्लेषण करेंगे। संख्यात्मक विश्लेषण निम्नलिखित विषयों पर केंद्रित है: 1) पेंडुलम दोलन अवधि की भविष्यवाणी करें 2) प्रोग्राम के रूप में पेंडुलम सरल हार्मोनिक आंदोलन प्रयोग डेटा एकत्र करें 3) समूह डेटा के लिए किमी का उपयोग करें और विश्लेषण प्रक्रिया में आउटलेर्स को हटा दें 4) अनुमान लगाने के लिए कम समय के एफएफटी का उपयोग करें लोलक दोलन आवृत्ति
आपूर्ति
ब्लूटूथ माप उपकरण
Android फ़ोन ऐप: Google playstore पर जाएं, M2ROBOTS सर्च करें और कंट्रोल ऐप इंस्टॉल करें। यदि Google playstore तक पहुंचना मुश्किल है, तो वैकल्पिक ऐप डाउनलोड विधि के लिए मेरे व्यक्तिगत होमपेज पर जाएं
लकड़ी की छड़
कुछ 3डी प्रिंटेड पार्ट्स
देखा ब्लेड या इसी तरह की धातु सामग्री
चरण 1: पेंडुलम क्या हैं? इसे कैसे मॉडल करें?
आपके पाठ्यक्रम भौतिकी पुस्तक सहित, पेंडुलम समीकरण व्युत्पत्ति का परिचय देने वाले कई लेख और पुस्तकें हैं। इस तरह की सामग्री को यहां दोबारा न दोहराया जाए तो बेहतर होगा। "सरल हार्मोनिक गति" के विषय के संबंध में केवल अंतिम निष्कर्ष यहां सूचीबद्ध है। एक पेंडुलम की अवधि जानने के लिए, हमें केवल पेंडुलम की लंबाई जानने की जरूरत है, जिसे मीटर में "एल" के रूप में दर्शाया गया है।
यदि हम यथोचित रूप से सुनिश्चित हैं कि वजन लगभग पूरी तरह से एक धुरी में लटके हुए भारहीन कॉर्ड के अंत में स्थित है, और पेंडुलम छोटे कोणों पर झूल रहा है, मान लीजिए कि 15° से कम है, तो ऐसे पेंडुलम की अवधि T1 द्वारा दी गई है:
T1 = 2*pi*(l/g)^0.5
g = गुरुत्वीय त्वरण, लगभग 9.8 m/s^2
यदि भारहीन कॉर्ड को एक कठोर वर्दी रॉड से बदल दिया जाता है, फिर से लंबाई l, इसकी सरल हार्मोनिक गति अवधि T2 द्वारा दी जाती है T1 = 2*pi*(2l/3g)^0.5
प्रभावी रूप से इसकी अवधि एक भारहीन कॉर्ड पेंडुलम के समान होती है जो कठोर समान छड़ की लंबाई का दो तिहाई होता है।
यह पृष्ठभूमि है, और हम अपने प्रयोग की तैयारी शुरू कर सकते हैं।
चरण 2: हार्डवेयर बिल्डिंग के लिए पुर्जे तैयार करें



पेंडुलम संरचना बनाने के लिए, हम कुछ हिस्सों को 3 डी प्रिंट करते हैं, और हमारे पास पहले से मौजूद कुछ को रीसायकल करते हैं। समग्र पेंडुलम संरचना चित्र 1 में दिखाई गई है। यह कुछ हाथ से तैयार किए गए हिस्सों के साथ 3 डी प्रिंट भागों का मिश्रण है और लोव से लकड़ी की छड़ का एक लंबा टुकड़ा है।
Fig.2 में 3D प्रिंटेड हिस्सा एक दरवाजे के ऊपरी किनारे पर लटका हुआ है, क्योंकि हमारा दरवाजा हमारे लिए कुछ लटकाने के लिए एक आसान सपाट सतह है। एसटीएल फ़ाइल डाउनलोड लिंक:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Fig.3 में हरा हिस्सा लकड़ी की छड़ को एक ब्लेड से जोड़ता है, और ब्लेड पहले के 3D प्रिंटेड डोर हैंगर पर लगे रेल के दो टुकड़ों के ऊपर बैठता है। एसटीएल फ़ाइल डाउनलोड लिंक:
रेल के दो टुकड़े एक पुराने आरा ब्लेड को आधे में तोड़कर बनाए गए हैं, चित्र 4 देखें। चित्र 2 में भाग ने उनके लिए सही स्लॉट आकार तैयार किया है। आदर्श रूप से हम एक फ़ाइल का उपयोग करके उन दो आरा ब्लेड में "वी" आकार का पायदान बना सकते हैं। एक काफी तेज धार वाली धातु, जैसे कि एक किनारे वाला रेजर ब्लेड, या कोई हाथ से बना धातु का टुकड़ा, "वी" आकार के पायदान के अंदर बैठ सकता है। हमें एक छोटे संपर्क क्षेत्र की आवश्यकता है क्योंकि झूलते समय खोई हुई गतिज ऊर्जा को कम करना है।
Fig.5 में अंतिम 3D मुद्रित भाग इलेक्ट्रॉनिक माप उपकरण को पकड़ने के लिए एक छोटी ट्रे है।
डाउनलोड लिंक:
ब्लूटूथ माप उपकरण कोण अनुमान, जाइरो माप और एक्सेलेरोमीटर माप उत्पन्न करता है। ये सभी डेटा ब्लूटूथ वायरलेस लिंक के माध्यम से हमें उपलब्ध हैं।
हम इस उपकरण को पेंडुलम आर्म की अलग-अलग स्थिति में तैनात करके कई प्रयोग करने जा रहे हैं, और अंतर देखें।
चरण 3: प्रयोग डेटा संग्रह



इससे पहले कि हम अधिग्रहीत डेटासेट का विश्लेषण करें, प्रायोगिक डेटा संग्रह के लिए दो उल्लेखनीय विधियाँ हैं:
1) अपने फोन के एसडी कार्ड में संग्रहीत डेटा फ़ाइल में उपकरण द्वारा उत्पादित सभी मापों को लॉग करने के लिए आवश्यकता अनुभाग में निर्दिष्ट एंड्रॉइड फोन ऐप का उपयोग करें। हम फाइल को कॉपी कर सकते हैं और जानकारी को पोस्ट प्रोसेस कर सकते हैं।
2) उपकरण से ब्लूटूथ कनेक्शन स्थापित करने के लिए ब्लूटूथ सक्षम कंप्यूटर, पीसी, लैपटॉप या रास्पबेरीपी मिनी-कंप्यूटर का उपयोग करें और रीयलटाइम या ऑफलाइन विश्लेषण के लिए डेटा पढ़ें।
प्रत्येक विधि के लिए पेशेवरों और विपक्ष दोनों मौजूद हैं, हम दोनों को आजमाने जा रहे हैं और इस निर्देश में अंतर बताएंगे।
विधि (1) के लिए एंड्रॉइड ऐप का उपयोग करते हुए, एक बार जब हम एंड्रॉइड ऐप कंट्रोल इंटरफेस में होते हैं, तो ब्लूटूथ माप उपकरण से एंड्रॉइड फोन पर भेजे गए टेलीमेट्री डेटा को m2flightDatayyyymmdd_hhmmss.txt नामक एक डेटालॉग फ़ाइल में रिकॉर्ड किया जाएगा। यह आपके Android फ़ोन के डाउनलोड/m2LogFiles फ़ोल्डर में पाया जा सकता है। फ़ोल्डर "डाउनलोड" आपके फ़ोन के Android OS में पहले से मौजूद फ़ोल्डर है और "m2LogFiles" एक फ़ोल्डर है जिसे ऐप ने बनाया है। फ़ाइल नाम सामग्री yyyymmdd_hhmmss फ़ाइल नाम में प्रयोग प्रारंभ समय (वर्ष, माह, दिन, घंटा, मिनट और सेकंड) को एन्कोड करने का तरीका है।
लॉग फ़ाइल में प्रत्येक पंक्ति एक रिकॉर्ड है। यह इवेंट टाइमस्टैम्प, प्रस्तावना स्ट्रिंग "ईम:" से शुरू होता है, इसके बाद 4 ट्रिपल डेटा होता है, जो हैं:
एक्सेलेरोमीटर XYZ एक्सिस रीडिंग इन रॉ सेंसर हार्डवेयर रजिस्टर रीडबैक वैल्यू
कच्चे सेंसर हार्डवेयर रजिस्टर रीडबैक मानों में Gyroscope XYZ अक्ष पढ़ना
कच्चे सेंसर हार्डवेयर रजिस्टर रीडबैक मानों में मैग्नेटोमीटर XYZ अक्ष पढ़ना
ऑनबोर्ड अनुमानित रोल/पिच/कच्चे डिग्री में
कंप्यूटर पायथन प्रोग्राम का उपयोग करके बनाई गई डेटाफाइल समान डेटा फ़ाइल प्रारूप का उपयोग करेगी, ताकि डेटा विश्लेषण चरण में हम जिस प्रोग्राम का उपयोग करते हैं, वह हमारे पायथन प्रोग्राम या एंड्रॉइड ऐप द्वारा उत्पादित डेटा स्रोत से परेशान न हो।
आइए विधि (2) का उपयोग करके कोडिंग शुरू करें।
ब्लूटूथ माप उपकरण के साथ बातचीत करने के लिए, एसडीके के दो स्वाद प्रदान किए जाते हैं:
1) पायथन एसडीके, जिसे "pip3 install m2controller" द्वारा स्थापित किया जा सकता है, python3 उपयोग की जाने वाली भाषा है। उपयोगकर्ता एप्लिकेशन कोड के उदाहरण https://github.com/xiapeiqing/m2robots/tree/maste… में संग्रहीत हैं। इस प्रयोग के लिए, हम अजगर स्क्रिप्ट pendulum1.py का उपयोग करेंगे।
2) जावा एसडीके, जिसका उपयोग इस निर्देश में नहीं किया गया है क्योंकि हम बाद में प्राप्त पेंडुलम डेटा का विज़ुअलाइज़ेशन और विश्लेषण चाहते हैं, जो जावा में प्रोग्राम करने के लिए हमारे लिए थोड़ा अधिक प्रयास कर सकता है।
Python3 डेटा संग्रह प्रोग्राम स्रोत कोड में कोड कार्यक्षमता विवरण के लिए कई टिप्पणियाँ हैं। स्रोत कोड का एक स्नैपशॉट यहां दिया गया है।
#!/usr/bin/env python# -*- कोडिंग: UTF-8 -*- m2controller से m2controller आयात m2controller से आयात m2Const आयात संकेत आयात समय आयात डेटाटाइम आयात usrCfg आयात पेंडुलम2
requestExit = गलत
################################################################
# हम उसी लॉग फ़ाइल नामकरण परंपरा का उपयोग करना चाहते हैं ताकि डेटा विश्लेषण मॉड्यूल, pendulum2.py, हमें लॉग डेटा फ़ाइल प्राप्त करने के तरीके से अनजान हो सके ################ ########################################## logfilename = " m2flightData%s.txt"%(datetime.datetime.fromtimestamp(time.time()).strftime('%Y%m%d_%H%M%S')) dataLogfile = open(logfilename, "w")
डीईएफ़ सिग्नल_हैंडलर (सिग, फ्रेम):
वैश्विक अनुरोध एक्ज़िट प्रिंट ('प्रोग्राम निष्पादन से बाहर निकलने के लिए उपयोगकर्ता Ctrl-C') requestExit = ट्रू सिग्नल। सिग्नल (सिग्नल। सिगिनट, सिग्नल_हैंडलर)
################################################################
# हर माप डेटा 20Hz दर पर उपलब्ध होने पर, यह "कॉलबैक" फ़ंक्शन बुलाया जाएगा ########################## ############################## डीईएफ़ कॉलबैकफ़ंक (टेलीमेट्री): strTimeStamp = datetime.datetime.fromtimestamp (time.time ()).strftime('%H:%M:%S.%f')[:-3] dataStr = "%s, eam:%d, %d, %d, %d, %d, %d, %d, %d, %d, %2.1f, %2.1f, %2.1f\n"%(strTimeStamp, टेलीमेट्री['m_fAccelHwUnit'][0], टेलीमेट्री['m_fAccelHwUnit'][1], टेलीमेट्री['m_fAccelHwUnit'][2], टेलीमेट्री['m_fGyroHwUnit'][0], टेलीमेट्री['m_fGyroHwUnit'][1], टेलीमेट्री['m_fGyroHwUnit'][2], टेलीमेट्री['m_fMagHwUnit'][0], टेलीमेट्री['m_fMagHwUnit'][1], टेलीमेट्री['m_fMagHwUnit'][2], टेलीमेट्री['m_fRPYdeg'][0], टेलीमेट्री['m_fRPYdeg'][1], टेलीमेट्री['m_fRPYdeg'][2]) ## ############################################# ############ # हम डेटा स्ट्रिंग को स्क्रीन पर प्रिंट करते हैं और उन्हें लॉग फ़ाइल में सहेजते हैं #################### ###################################### प्रिंट (dataStr) dataLogfile.writelines(डेटा एसटीआर)
################################################################
# कंट्रोलर को इनिशियलाइज़ करें, BleMACaddress को अपने डिवाइस के मैक एड्रेस के रूप में सेट करना याद रखें ############################# ############################ # TODO: यदि उपयोगकर्ता द्वारा सेट नहीं किया जा रहा है तो BleMACaddress को इनिशियलाइज़ करें। कंट्रोलर = m2controller. BleCtrller(m2Const.etDebian, कॉलबैकफंक, usrCfg. BleMACaddress) कंट्रोलर.कनेक्ट () जबकि ट्रू: ####################### ################################## # पेंडुलम माप से बनाए और भेजे गए माप डेटा की प्रतीक्षा करें उपकरण ############################################ ############## नियंत्रक.m_CommsTunnel.waitForNotifications(1.0) अगर अनुरोध से बाहर निकलें: ###################### #################################### # जब हम डेटा लॉगिंग समाप्त करते हैं तो यहां हाउस कीपिंग का काम होता है ############################################# ############# कंट्रोलर.स्टॉप () dataLogfile.close() ब्रेक
################################################################
# डेटा संग्रह पूरा हुआ, अब लॉग डेटा का विश्लेषण करते हैं ################################# ####################### pendulum2.parseDataLogFile(logfilename)
लंबी अवधि के अपडेट के लिए, कृपया चेकआउट करें
अब इसकी संचालन विधि की व्याख्या करते हैं। यह पायथन प्रोग्राम एक पाइप इंस्टाल करने योग्य पैकेज के ऊपर लिखा गया है, जिसका नाम m2controller है। निचले स्तर का पैकेज कॉलबैक तंत्र प्रदान करता है, ताकि प्रत्येक प्राप्त माप अपडेट हमारे द्वारा लिखे गए कॉलबैक फ़ंक्शन को ट्रिगर करे, और डेटा को स्थानीय लॉग फ़ाइल में सहेजे। लॉग फ़ाइल डेटा सामग्री का प्रारूप एंड्रॉइड साथी ऐप द्वारा निर्मित के समान है, ताकि पाइथन प्रोग्राम या एंड्रॉइड साथी ऐप द्वारा बनाई गई डेटा लॉग फ़ाइल विनिमय योग्य हो।
ऑपरेटिंग सिस्टम द्वारा कब्जा कर लिया गया उपयोगकर्ता ctrl-C सिग्नल प्रोग्राम को पास कर दिया जाता है, और माप डेटा के नए आगमन की प्रतीक्षा में अनंत लूप को रोक देता है।
अब तक, लॉग फ़ाइल सफलतापूर्वक बनाई गई है, और यह प्रोग्राम हमारे प्रयोग परिणामों का अध्ययन करने के लिए विश्लेषण कार्यक्रम को बुलाएगा।
यहां दो प्रयोग हैं, और तुलना विभिन्न स्थानों पर एक 7 ग्राम डिवाइस को जोड़कर बहुत ही उल्लेखनीय अंतर दिखाती है।
Fig.2 में, हम इस ब्लूटूथ माप उपकरण के वास्तविक वजन को निर्धारित करने के लिए एक पैमाने का उपयोग करते हैं।
Fig.3 पेंडुलम सेटअप को दर्शाता है जहां 7 ग्राम डिवाइस पेंडुलम के निचले सिरे से जुड़ा हुआ है। Fig.4 में सेटअप कॉन्फ़िगरेशन में 7gram द्रव्यमान है जो स्विंगिंग पिवट के बहुत करीब स्थित है।
Fig.5 पेंडुलम संरचना का एक नज़दीकी दृश्य है।
चरण 4: डेटा विश्लेषण



ब्लूटूथ माप उपकरण का वजन ~ 7 ग्राम होता है, जिसका वजन ~ 1.6 मीटर लंबी लकड़ी की छड़ी से बहुत कम होता है। "कठोर वर्दी रॉड" की धारणा का प्रयोग करें, और हमारे पास यह पेंडुलम अवधि समीकरण है, T1 = 2*pi*(2l/3g)^0.5
गुरुत्वाकर्षण स्थिरांक प्राप्त करने के लिए, हम 9.8m/s^2 का उपयोग कर सकते हैं। लेकिन किसी भी भौगोलिक स्थान पर अधिक सटीक गुरुत्वाकर्षण स्थिरांक इस वेब सेवा से प्राप्त किया जा सकता है:
www.wolframalpha.com/widgets/view.jsp?id=e…
सैन फ्रांसिस्को के लिए, यह 9.81278m/s^2. है
पेंडुलम की लंबाई ६४.५'' मापी जाती है
2*pi*sqrt(2*64.5*0.0254/(3*9.81278)) 2.0962(सेकंड) की अपेक्षित पेंडुलम अवधि देता है।
आइए देखें कि यह हमारे प्रयोगों से सहमत है या नहीं।
पहले प्रयोग में, पेंडुलम सेटअप में पेंडुलम के निचले सिरे से जुड़ा 7 ग्राम उपकरण होता है। मेरी लॉग फ़ाइल इसमें डाउनलोड की जा सकती है:
xiapeiqing.github.io/doc/kits/pendulum/pen…
इसका नाम बदलकर "PendulumTestData.txt" कर दें और इसे पायथन एनालिसिस प्रोग्राम के उसी फोल्डर में रख दें। स्रोत कोड का एक स्नैपशॉट यहां दिया गया है।
#!/usr/bin/env python# -*- कोडिंग: UTF-8 -*- आयात csv आयात matplotlib.pyplot plt plt.style.use('seaborn-whitegrid') के रूप में numpy डेटाटाइम आयात डेटाटाइम से np के रूप में आयात करें, sklearn.cluster से एसएनएस के रूप में टाइमडेल्टा आयात सीबॉर्न। संग्रह आयात से KMeans आयात काउंटर ############################## ########################## # यह फ़ंक्शन डेटा फ़ाइल विश्लेषण कार्य चलाता है ############ ############################################# ## def parseDataLogFile(datafilename): #################################### ##################### # कॉमा सेपरेटेड डेटा लॉग फ़ाइल (सीएसवी) में डेटा निकालें और प्रत्येक कॉलम में सामग्री को एक फ्लोट-टाइप वेरिएबल में सहेजें ## ############################################# ############ ओपन (डेटाफाइलनाम) के साथ csvfile: readCSV = csv.reader(csvfile, delimiter=', ') टाइमस्टैम्प = fAccelHwUnit_x = fAccelHwUnit_y = fAccelHwUnit_z = fGyroHwUnit_x = fGyroHwUnit_y = fGyroHwUnit_z = fMagHwUnit_x = fMagHwUnit_y = fMagHwUni t_z = fRPYdeg_r = fRPYdeg_p = fRPYdeg_y = readCSV में पंक्ति के लिए: कोशिश करें: x = datetime.strptime(row[0].split(', ')[0], '%H:%M:%S.%f') टाइमस्टैम्पS.append(timedelta(hours=x.hour, minutes=x.minute, सेकंड्स=x.second, microseconds=x.microsecond).total_seconds()) fAccelHwUnit_x.append(float(row) [1][4:])) fAccelHwUnit_y.append(float(row[2])) fAccelHwUnit_z.append(float(row[3])) fGyroHwUnit_x.append(float(row[4])) fGyroHwUnit_y.append(float) (पंक्ति[5])) fGyroHwUnit_z.append(float(row[6])) fMagHwUnit_x.append(float(row[7])) fMagHwUnit_y.append(float(row[8])) fMagHwUnit_z.append(float(row) [९])) fRPYdeg_r.append(float(row[10])) fRPYdeg_p.append(float(row[11])) fRPYdeg_y.append(float(row[12])) को छोड़कर: टाइमस्टैम्प पास करें = np.asarray(timestamps) timestamps = timestamps - timestamps [0] fAccelHwUnit_x = np.asarray (fAccelHwUnit_x) fAccelHwUnit_y = np.asarray (fAccelHwUnit_y) fAccelHwUnit_z = np.asarray (fAccelHwUnit_z) fGyroHwUnit_x = np.asarray (fGyroHwUnit_x) fGyroHwUnit_y = np.asarray (fGyroHwUnit_y) fGyroH wUnit_z = np.asarray (fGyroHwUnit_z) fMagHwUnit_x = np.asarray (fMagHwUnit_x) fMagHwUnit_y = np.asarray (fMagHwUnit_y) fMagHwUnit_z = np.asarray (fMagHwUnit_z) fRPYdeg_r = np.asarray (fRPYdeg_r) fRPYdeg_p = np.asarray (fRPYdeg_p) fRPYdeg_p = fRPYdeg_p - np.mean(fRPYdeg_p) fRPYdeg_y = np.asarray(fRPYdeg_y)
################################################################
# हमें सटीक दोलन अवधि के अनुमान के लिए नमूना आवृत्ति का सटीक अनुमान लगाने की आवश्यकता है ############################### ######################### FsHz = getSamplingIntervalS(timestampS) ############### ################################################ # उपयोग पेंडुलम अवधि विश्लेषण के लिए रवैया शीर्षक संदर्भ प्रणाली आउटपुट में पिच घटक ############################### ######################## विश्लेषण_टाइम सीक्वेंस (टाइमस्टैम्प, fRPYdeg_p, FsHz, 'पिच') ########## ############################################# ### # पेंडुलम अवधि विश्लेषण के लिए एक्सेलेरोमीटर कच्चे माप आउटपुट का उपयोग करें ################################ ######################### विश्लेषण_समय अनुक्रम (टाइमस्टैम्प, fAccelHwUnit_x, FsHz, 'accel') ########### ############################################# ### # पेंडुलम अवधि विश्लेषण के लिए जाइरो कच्चे माप आउटपुट का उपयोग करें ############################### ######################## विश्लेषण_टाइम सीक्वेंस (टाइमस्टैम्प, fGyroHwUnit_y, FsHz, ' gyro') प्रिंट ('हो गया, बधाई:-)') plt.show() ########################## ############################### # ब्लूटूथ संचार प्रक्रिया में, एक दुर्लभ मौका है कि डेटा कॉम पैकेट कर सकता है खो जाना # हम 20Hz मापन डेटा को आउटलेर्स से अलग करने के लिए K-मीन का उपयोग करते हैं, जो कि गिराए गए पैकेट के कारण होता है # "अधिक विवरण के लिए सिग्नल और सिस्टम" में गोता लगाएँ ############### ########################################## डीईएफ़ getSamplingIntervalS (टाइमस्टैम्पएस): plt.figure() sampleIntervalS = np.diff(timestampS) sns.distplot(sampleIntervalS) plt.ylabel('histogram') plt.xlabel('measurement interval(s)') clusterCnt = 5 km = KMeans(n_clusters = क्लस्टरCnt) km.fit(sampleIntervalS.reshape(-1, 1)) centroids = km.cluster_centers_ elemCnt = काउंटर (km.labels_) घटनाCnt = ii के लिए रेंज (clusterCnt) में: घटनाCnt.append(elemCnt[ii)]) FsHz = 1/centroids [occurrenceCnt.index(max(occurrenceCnt))] FsHz लौटाएं
################################################################
# स्पेक्ट्रोमीटर का उपयोग करें, यानी आवृत्ति घटक प्राप्त करने के लिए कम समय एफएफटी, पीक बिन पेंडुलम दोलन का हमारा सबसे अच्छा अनुमान है ####################### ################################## डीईएफ़ एनालिसिस_टाइम सीक्वेंस (टाइमस्टैम्पएस, टाइमसेकडाटा, एफएसएचजेड, स्ट्रकॉममेंट): अंजीर, (ax1, ax2) = plt.subplots(nrows=2) ax1.plot(timestampS, timeSeqData, मार्कर='ओ', मार्करफेसकलर='ब्लू', मार्करसाइज=2, रंग='स्काईब्लू', लाइनविड्थ = 1) ax1.set_title("पेंडुलम टाइम डोमेन मेजरमेंट --%s"%strComment) ax1.set_xlabel("सैंपलिंग टाइम(सेकंड)") ax1.set_ylabel(strComment); NFFT = 2048 # विंडोिंग सेगमेंट की लंबाई
Pxx, freqs, bins, im = ax2.specgram(timeSeqData, NFFT=NFFT, Fs=FsHz, noverlap=NFFT/2)
ax2.set_title ("स्पेक्ट्रोग्राम") ax2.set_xlabel ("नमूने") ax2.set_ylabel ("आवृत्ति (हर्ट्ज)");
# 'स्पेकग्राम' विधि 4 ऑब्जेक्ट लौटाती है। वे:
# - Pxx: पीरियडोग्राम # - फ़्रीक्वेंसी: फ़्रीक्वेंसी वेक्टर # - बिन्स: टाइम बिन्स के केंद्र # - im: matplotlib.image. AxesImage इंस्टेंस प्लॉट में डेटा का प्रतिनिधित्व करता है pkresult = np.where(Pxx == np.amax(Pxx)) oscFreqHz = freqs[pkresult[0][0] प्रिंट ('पेंडुलम दोलन आवृत्ति (Hz) =% f, अवधि (सेक) =% f, अनुमान डेटा स्रोत:% s'% (oscFreqHz, 1/oscFreqHz, strComment)) वापसी 1/oscFreqHz
################################################################
# क्या हमें इस कार्यक्रम को स्वतंत्र रूप से चलाना चाहिए, अर्थात, pendulum1.py द्वारा नहीं बुलाया जा रहा है, # हम विश्लेषण के लिए एक डिफ़ॉल्ट लॉग डेटा फ़ाइल नाम परिभाषित करते हैं ################## ####################################### अगर _name_ == "_main_ ": defaultFilename = './PendulumTestData.txt' आयात os.path अगर os.path.isfile(defaultFilename): parseDataLogFile(defaultFilename) अन्य: प्रिंट ("डिफ़ॉल्ट लॉग फ़ाइल %s मौजूद नहीं है"%defaultFilename)
लंबी अवधि के अपडेट के लिए, कृपया चेकआउट करें
स्रोत कोड में विस्तृत टिप्पणियाँ हैं, आइए यहाँ गणितीय अनुमान का एक उच्च स्तरीय सारांश दें।
1) हम सबसे पहले "सीएसवी" नामक पायथन पैकेज का उपयोग करके कंप्यूटर में सीएसवी फ़ाइल सामग्री को पढ़ते हैं। हमारे पास आवधिक माप है।
21:34:26.362, ईएएम:0, -128, 14464, -8, 144, -96, 2112, -1280, 1664, -0.5, -5.5, 40.5
21:34:26.373, ईएएम:128, 0, 14272, -8, 136, 40, 2112, -1280, 1664, -0.5, -6.5, 40.0
21:34:26.412, ईएएम:448, -64, 14208, -8, 136, 24, 2176, -1280, 1664, -0.5, -7.5, 40.5
21:34:26.462, ईएएम:448, -128, 14272, -8, 120, 16, 2176, -1280, 1664, -0.5, -8.0, 40.5
2) चूंकि माप दर इतनी महत्वपूर्ण है और सीधे पेंडुलम अवधि अनुमान त्रुटि का परिचय देती है, हम उनका अनुमान लगाना चाहते हैं। हमारा नाममात्र माप अंतराल 50ms, यानी 20Hz है। सभी मापों पर औसत ठीक लगता है, लेकिन हम कभी-कभी डेटा ट्रांसमिशन पैकेट खो देते हैं, अपडेट अंतराल 100ms या 150ms हो जाता है, …
यदि हम इन आंकड़ों की घटना की साजिश करते हैं, तो चित्र 1 देखें, एक मानव के रूप में, हम आसानी से 0.05 सेकेंड का नेत्रगोलक मान प्राप्त कर सकते हैं। हालाँकि, क्या हम इससे बेहतर कर सकते हैं?
हमें औसत गणना के लिए केवल अच्छे लोगों का चयन करने के लिए वर्गीकरण पद्धति का उपयोग करने की आवश्यकता है। पायथन में KMeans नाम का टूलबॉक्स है जो हमें क्लस्टरिंग, या वर्गीकरण में मदद करता है। इन अवधारणाओं का उपयोग कई बड़े डेटा और एआई क्षेत्रों में किया जाता है।
3) चित्र 2 में दो चित्र हैं। शीर्ष प्लॉट हमारे स्विंगिंग कोण माप का एक समय-डोमेन अनुक्रम है। सेकंड में x-अक्ष टाइमस्टैम्प को संदर्भित करके, हम ५०सेकंड में लगभग २२.५ चक्र पढ़ सकते हैं, जो २.२२ सेकंड के पेंडुलम अवधि का अनुवाद करता है। क्या इस प्रक्रिया को स्वचालित करने और अधिक सटीक अनुमान लगाने का कोई तरीका है? हां, हम स्पेक्ट्रोग्राम नामक गणितीय उपकरण का उपयोग कर सकते हैं, जो माप डेटा के एक छोटे से हिस्से का उपयोग करता है और हमें इसकी आवृत्ति बताता है, नीचे दिया गया चित्र देखें। सबसे गहरी रेखा के लिए y-अक्ष रीडिंग पेंडुलम दोलन आवृत्ति है। एक क्षैतिज रेखा होने से पुष्टि होती है कि पूरे प्रयोग के दौरान पेंडुलम दोलन बिल्कुल नहीं बदला। दोलन आवृत्ति का व्युत्क्रम मान पेंडुलम दोलन अवधि है।
कार्यक्रम द्वारा बनाई गई अंतिम रिपोर्ट एक पाठ सारांश है:
पेंडुलम दोलन आवृत्ति (हर्ट्ज) = 0.449224, अवधि (सेक) = 2.226059, अनुमान डेटा स्रोत: पिच
हम अपने पहले के नेत्रगोलक हाथ गणना परिणाम, 2.22 सेकंड, प्रोग्राम की गणना मूल्य के साथ काफी संगत है।
2.0962 (सेकंड) सैद्धांतिक रूप से गणना मूल्य की तुलना में, हमारे पास ~ 5% शेष त्रुटि है। उनसे कैसे छुटकारा पाया जाए? याद रखें धारणा "कठोर वर्दी रॉड" है? 7 ग्राम अतिरिक्त वजन भी तुच्छ लगता है, यह शेष त्रुटि का सबसे बड़ा कारण है।
अब हम डिवाइस को धुरी के करीब ले जाते हैं। क्लोज़-अप फ़ोटो के लिए पिछला चरण देखें। मेरे द्वारा बनाई गई लॉग फ़ाइल यहाँ डाउनलोड की जा सकती है:
xiapeiqing.github.io/doc/kits/pendulum/pen…
एक ही विश्लेषण चरण चलाएं, और हमें 2.089867 (सेक) की अवधि मिलती है, चित्र 3 देखें, जो लगभग सैद्धांतिक भविष्यवाणी के समान है। महान!
चूंकि हमारे पास न केवल स्विंगिंग कोण माप है, बल्कि एक ही दर पर जाइरोस्कोपिक माप और एक्सेलेरोमीटर माप भी है। अन्य दो मापों के लिए समान विश्लेषण चलाएं, हमें चित्र 4 और 5 में परिणाम मिलते हैं। तीनों माप स्रोतों के अनुमान सहमत हैं, जो हमें अपने प्रयोग की सफलता पर अधिक आश्वस्त करते हैं।
यहाँ अजगर प्रोग्राम के अंतिम आउटपुट के रूप में परिणाम चल रहा है:
पेंडुलम दोलन आवृत्ति (हर्ट्ज) = ०.४७८४९९, अवधि (सेक) = २.०८९८६७, अनुमान डेटा स्रोत: पिच
पेंडुलम दोलन आवृत्ति (हर्ट्ज) = ०.४७८४९९, अवधि (सेक) = २.०८९८६७, अनुमान डेटा स्रोत: त्वरण
पेंडुलम दोलन आवृत्ति (हर्ट्ज) = ०.४७८४९९, अवधि (सेक) = २.०८९८६७, अनुमान डेटा स्रोत: जाइरो
इस चरण में अंतिम विचार, विभिन्न इनपुट डेटा स्रोत का उपयोग करके अनुमान के परिणाम बिल्कुल समान कैसे हो सकते हैं? यह प्रति-अंतर्ज्ञान है। यह प्रश्न पाठकों पर छोड़ता हूँ। यहाँ एक संकेत है: याद रखें कि हम दोलन आवृत्ति का अनुमान लगाने के लिए कम समय के FFT का उपयोग कर रहे हैं? डिजिटल डोमेन में, आवृत्ति अनुमान एक अस्थायी संख्या अनुमान के बजाय असतत आवृत्ति डिब्बे में दिया जाता है।
चरण 5: भविष्य के कार्य अनुशंसाएँ
भविष्य के काम की सिफारिशों की कुछ श्रेणियां हैं।
पहले चरण में, हम अपनी प्रयोग त्रुटि को ~5% से 1% से कम करने का प्रबंधन करते हैं, क्या हम इससे बेहतर कर सकते हैं? दोलन परिमाण को देखते हुए तेजी से घटता है, एक योगदान कारक पेंडुलम को झूलते समय होने वाली हवा का खिंचाव हो सकता है। पेंडुलम के क्रॉस सेक्शन को सुव्यवस्थित आकार के रूप में संशोधित करने की आवश्यकता हो सकती है ताकि वायुगतिकीय ड्रैग को कम किया जा सके।
क्या हम निरंतर शिखर-परिमाण सिग्नल को आउटपुट करने के लिए अनुकूली फ़िल्टर तकनीकों का उपयोग करके सीखे गए समय-भिन्न लाभ को लागू कर सकते हैं। इस बीच, बाह्य बलों के परिमाण क्षीणन को सहसंबंधित करें।
हम "सरल हार्मोनिक आंदोलन" की तुलना में शायद ही कुछ आसान पा सकते हैं। क्या हम उन सुविधाओं का उपयोग कर सकते हैं जो हम पेंडुलम का विश्लेषण कुछ अधिक जटिल, एक खेल गतिविधि, एक जल रॉकेट लॉन्च अनुक्रम, आदि का विश्लेषण करने के लिए करते हैं?
हैप्पी हैकिंग
सिफारिश की:
एक प्रायोगिक लैंप के एलईडी चमकदार प्रवाह का अध्ययन करने के लिए गाऊसी और परबोला: 6 कदम

एक प्रायोगिक लैंप के एलईडी चमकदार प्रवाह का अध्ययन करने के लिए गाऊसी और परबोला: सभी निर्माताओं और निर्देश के हलचल समुदाय को नमस्कार। इस बार मेरेनेल रिसर्च आपके लिए एक शुद्ध शोध समस्या और गणित के साथ इसे हल करने का एक तरीका लाएगा। मुझे यह समस्या थी जब मैं आरजीबी एलईडी लैंप के एलईडी फ्लक्स की गणना कर रहा था
आपकी हृदय गति को मापना आपकी उंगली की नोक पर है: हृदय गति निर्धारित करने के लिए फोटोप्लेथिस्मोग्राफी दृष्टिकोण: 7 कदम

आपकी हृदय गति को मापना आपकी उंगली की नोक पर है: Photoplethysmography दृष्टिकोण हृदय गति निर्धारित करने के लिए दृष्टिकोण: एक photoplethysmograph (PPG) एक सरल और कम लागत वाली ऑप्टिकल तकनीक है जिसका उपयोग अक्सर ऊतक के सूक्ष्म संवहनी बिस्तर में रक्त की मात्रा में परिवर्तन का पता लगाने के लिए किया जाता है। यह ज्यादातर त्वचा की सतह पर माप करने के लिए गैर-आक्रामक रूप से उपयोग किया जाता है, आमतौर पर
धीमी गति वाले वीडियो के लिए उच्च गति वाली घड़ी: 4 कदम

स्लो-मोशन वीडियो के लिए हाई-स्पीड क्लॉक: आधुनिक स्मार्टफोन वाले लगभग हर किसी के पास हाई-स्पीड कैमरा होता है जिसका इस्तेमाल शानदार स्लो-मोशन वीडियो बनाने के लिए किया जा सकता है। लेकिन अगर आप यह मापना चाहते हैं कि वास्तव में उस साबुन के बुलबुले को फूटने में या उस तरबूज को फटने में कितना समय लगता है, तो आप
सरल ईसीजी और हृदय गति डिटेक्टर: 10 कदम
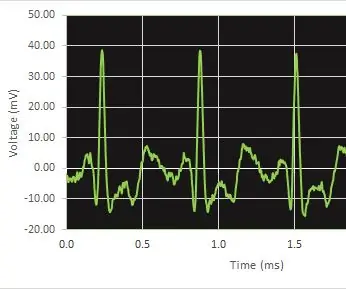
सरल ईसीजी और हृदय गति डिटेक्टर: सूचना: यह एक चिकित्सा उपकरण नहीं है। यह केवल नकली संकेतों का उपयोग करके शैक्षिक उद्देश्यों के लिए है। यदि वास्तविक ईसीजी माप के लिए इस सर्किट का उपयोग कर रहे हैं, तो कृपया सुनिश्चित करें कि सर्किट और सर्किट-टू-इंस्ट्रूमेंट कनेक्शन उचित अलगाव का उपयोग कर रहे हैं
कैसे यूट पीसी को तेज गति दें, और सिस्टम के जीवन के लिए उस गति को बनाए रखें।: 9 कदम

यूट पीसी को तेजी से कैसे तेज करें, और सिस्टम के जीवन के लिए उस गति को बनाए रखें: यह एक ट्यूटोरियल है जिसे मैंने आपके द्वारा पहली बार खरीदे जाने की तुलना में तेजी से चलाने के लिए पीसी को साफ, ट्वीक और ऑप्टिमाइज़ करने के तरीके पर बनाया है। यह और इसे इस तरह बनाए रखने में मदद करने के लिए। मौका मिलते ही मैं तस्वीरें पोस्ट करूंगा, दुर्भाग्य से अभी मैं नहीं
