ट्रुथ टेबल्स सॉल्विंग: १० स्टेप्स

2024 लेखक: John Day | [email protected]. अंतिम बार संशोधित: 2024-01-30 09:19

एक सत्य तालिका किसी समस्या के सभी परिणामों की कल्पना करने का एक तरीका है। यह निर्देश सेट असतत गणित में आरंभ करने वाले लोगों के लिए बनाया गया है। हम आज एक उदाहरण समस्या के साथ अभ्यास करेंगे जो इन निर्देशों के लिए विशिष्ट है। टेबल की कल्पना करने के लिए आपको कुछ स्क्रैच पेपर और एक पेंसिल की आवश्यकता होगी। विषय के बारे में पूर्व ज्ञान रखने वाले लोगों के लिए इस समस्या को पूरा करने में लगभग 5 मिनट और शुरुआती लोगों के लिए लगभग 10 मिनट का समय लगना चाहिए।

इस निर्देश सेट के लिए, हम समस्या ~p q पर ध्यान केंद्रित करेंगे। हम इसका उपयोग सत्य तालिकाओं की व्याख्या करने के लिए आवश्यक कुछ प्रतीकों को पेश करने के लिए कर रहे हैं।

चरण 1: सत्य सारणी को समझना

एक सत्य तालिका किसी समस्या की सभी संभावनाओं की कल्पना करने का एक तरीका है। असतत गणित के लिए सत्य सारणी जानना एक बुनियादी आवश्यकता है। यहाँ, हम ~p q के सरल समीकरण के सभी परिणाम प्राप्त करेंगे।

चरण 2: प्रतीकों को जानना

सत्य तालिका में पहला कदम संकेतों को समझना है। इस विशेष समस्या में "~" का अर्थ निषेध है। "पी" और "क्यू" दोनों चर हैं। "Λ" "और" के बराबर है। इस समीकरण को "नहीं p और q" के रूप में पढ़ा जाता है, जिसका अर्थ है कि समीकरण सत्य है यदि p सत्य नहीं है और q सत्य है।

चरण 3: तालिका को स्वरूपित करना

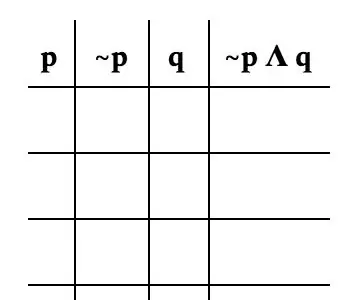
अब वास्तविक तालिका बनाने के लिए। प्रत्येक चर द्वारा समस्या को तोड़ना महत्वपूर्ण है। इस समस्या के लिए, हम इसे निम्नानुसार तोड़ेंगे: p, ~p, q, और ~p q। छवि इस बात का एक अच्छा उदाहरण है कि आपकी तालिका कैसी दिखनी चाहिए।

चरण 4: सही और गलत असाइन करना

चूँकि केवल दो चर हैं, प्रति चर केवल चार संभावनाएँ होंगी। p के लिए, हम इसे T (सत्य के लिए) द्वारा लिए गए आधे रिक्त स्थान और दूसरे आधे F (गलत के लिए) के साथ विभाजित करते हैं।

चरण 5: नकारात्मक

~p के लिए, आप विपरीत चिह्न लिखते हैं कि p, क्योंकि ~p, p के विपरीत है।

चरण 6: चर "क्यू"

q के लिए, आप प्रत्येक संभावित संयोजन प्राप्त करने के लिए T और F के बीच वैकल्पिक करते हैं। चूंकि समीकरण केवल ~p पर केंद्रित है, हम समीकरण की सच्चाई का निर्धारण करते समय p कॉलम को अनदेखा कर सकते हैं। "Λ" प्रतीक का अर्थ है कि समीकरण के सत्य होने के लिए ~p और q दोनों को सत्य होना चाहिए।

चरण 7: अंतिम कॉलम में असत्य को हल करना

पहली पंक्ति के लिए, चूंकि ~p F है और q T है, ~p Λ q इस परिदृश्य में F है कि ~p F है और q T है। एकमात्र परिदृश्य समीकरण T है जहां ~p T है और q है टी।

चरण 8: अंतिम कॉलम में सत्य ढूँढना

इसका मतलब है कि एकमात्र पंक्ति जो टी है वह तीसरी है।

चरण 9: तालिका को समाप्त करना

दोबारा जांचें कि आपकी तालिका सही है। आप ऐसा करते हैं कि आपके संकेत सही हैं और यह सुनिश्चित कर लें कि अंतिम कॉलम सही तरीके से किया गया है। अंतिम कॉलम चर से सभी संभावित क्रमपरिवर्तन का परिणाम है।

चरण 10: हो गया

अब जब आप जानते हैं कि एक बुनियादी सत्य तालिका कैसे बनाई जाती है, तो अभ्यास करते रहें! जितना अधिक आप अभ्यास करेंगे, आप उन्हें करने में उतने ही बेहतर होंगे।