विषयसूची:
- आपूर्ति
- चरण 1: सेटअप
- चरण 2: ऑसिलोस्कोप
- चरण 3: चरण की गणना करें
- चरण 4: कैलकुलेटर पर
- चरण 5: समीकरण हल करें
- चरण 6: परिकलित मान

वीडियो: जटिल गणित का उपयोग कर घटक प्रतिबाधा: 6 कदम

2024 लेखक: John Day | [email protected]. अंतिम बार संशोधित: 2024-01-30 09:19


यहाँ जटिल गणित समीकरणों का व्यावहारिक अनुप्रयोग है।
यह वास्तव में एक बहुत ही उपयोगी तकनीक है जिसका उपयोग आप पूर्व निर्धारित आवृत्तियों पर घटकों, या यहां तक कि एक एंटीना को चिह्नित करने के लिए कर सकते हैं।
यदि आप इलेक्ट्रॉनिक्स के साथ छेड़छाड़ कर रहे हैं तो आप प्रतिरोधों और ओम के नियम से परिचित हो सकते हैं। आर = वी / मैं अब आपको यह जानकर आश्चर्य हो सकता है कि जटिल प्रतिबाधा के लिए भी आपको बस इतना ही हल करना होगा! सभी प्रतिबाधा अनिवार्य रूप से जटिल हैं, अर्थात उनके पास एक वास्तविक और एक काल्पनिक भाग है। एक प्रतिरोधी के मामले में काल्पनिक (या प्रतिक्रिया) 0 है, तदनुसार वी और आई के बीच कोई चरण अंतर नहीं है, इसलिए हम उन्हें छोड़ सकते हैं।
जटिल संख्याओं पर एक त्वरित सारांश। कॉम्प्लेक्स का सीधा सा मतलब है कि संख्या दो भागों से बनी है, एक वास्तविक और एक काल्पनिक। सम्मिश्र संख्याओं का प्रतिनिधित्व करने के दो तरीके हैं, उदाहरण के लिए ऊपर की आकृति में, एक बिंदु को वास्तविक और काल्पनिक मूल्यों द्वारा परिभाषित किया जा सकता है, जैसे कि जहां पीली और नीली रेखाएं मिलती हैं। उदाहरण के लिए यदि नीली रेखा X अक्ष पर 4 और Y अक्ष पर 3 पर थी, तो यह संख्या 4 + 3i होगी, मैं इंगित करता हूं कि यह इस संख्या का काल्पनिक भाग है। उसी बिंदु को परिभाषित करने का दूसरा तरीका लाल रेखा की लंबाई (या आयाम) के साथ-साथ क्षैतिज के साथ कौन सा कोण बनाता है। ऊपर के उदाहरण में यह 5 <36.87 होगा।
या 36.87 डिग्री के कोण पर 5 की लंबाई वाली रेखा।
सभी मापदंडों के ऊपर के समीकरण में, R, V और I को एक काल्पनिक भाग के रूप में माना जा सकता है, जब प्रतिरोधों के साथ काम करते समय यह मान 0 होता है।
इंडक्टर्स या कैपेसिटर के साथ काम करते समय, या जब संकेतों के बीच एक चरण अंतर (डिग्री में) मापा जा सकता है, तो समीकरण वही रहता है लेकिन संख्या का काल्पनिक हिस्सा शामिल होना चाहिए। अधिकांश वैज्ञानिक कैलकुलेटर जटिल गणित के साथ काम करना बहुत आसान बनाते हैं, इस ट्यूटोरियल में मैं कैसियो fx-9750GII पर एक उदाहरण के माध्यम से काम करूंगा।
सबसे पहले, रोकनेवाला वोल्टेज विभक्त समीकरण पर एक पुनर्कथन।
आकृति के अनुसार-
Y पर वोल्टेज वर्तमान है I को R2. से गुणा किया जाता है
मैं वोल्टेज X है जो R1 और R2. के योग से विभाजित है
जब R2 अज्ञात होता है तो हम अन्य मानों, X, Y, R1 को माप सकते हैं और R2 को हल करने के लिए समीकरण को फिर से व्यवस्थित कर सकते हैं।
आपूर्ति
साइंटिफ़िक कैलकुलेटर
संकेतक उत्पादक
आस्टसीलस्कप
चरण 1: सेटअप

आइए मान लें कि हम 1 मेगाहर्ट्ज पर डिवाइस अंडर टेस्ट (डीयूटी) के अधिष्ठापन की गणना करना चाहते हैं।
सिग्नल जनरेटर को 1MHZ पर 5V के साइनसॉइडल आउटपुट के लिए कॉन्फ़िगर किया गया है।
हम 2k ओम प्रतिरोधों का उपयोग कर रहे हैं, और आस्टसीलस्कप चैनल CH1 और CH2. हैं
चरण 2: ऑसिलोस्कोप

जैसा कि चित्र में दिखाया गया है, हमें तरंगें मिलती हैं। एक चरण बदलाव को आस्टसीलस्कप पर 130ns से आगे बढ़ने के लिए देखा और मापा जा सकता है। आयाम 3.4V है। ध्यान दें, CH1 पर सिग्नल 2.5V होना चाहिए क्योंकि इसे वोल्टेज डिवाइडर के आउटपुट पर लिया जाता है, यहाँ इसे स्पष्टता के लिए 5V के रूप में दिखाया गया है, क्योंकि यह वह मान है जिसे हमें अपनी गणना में भी उपयोग करना चाहिए। यानी 5V अज्ञात घटक के साथ विभक्त के लिए इनपुट वोल्टेज है।
चरण 3: चरण की गणना करें

1 मेगाहर्ट्ज पर इनपुट सिग्नल की अवधि 1us है।
130ns 0.13 का अनुपात देता है। या 13%। 360 का 13% 46.6. है
5V सिग्नल को 0.. का कोण दिया जाता है क्योंकि यह हमारा इनपुट सिग्नल है और फेज़ शिफ्ट इसके सापेक्ष है।
3.4V सिग्नल को +46.6 का कोण दिया जाता है (+ का मतलब यह अग्रणी है, एक संधारित्र के लिए कोण नकारात्मक होगा)।
चरण 4: कैलकुलेटर पर


अब हम कैलकुलेटर में बस अपने मापा मूल्यों को दर्ज करते हैं।
आर 2k. है
वी 5 है (संपादित करें - वी 5 है, बाद में समीकरण में एक्स का उपयोग किया जाता है! परिणाम बिल्कुल वैसा ही है जैसा मेरे कैलकुलेटर में एक्स के रूप में 5 है)
Y चरण कोण के साथ हमारा मापा वोल्टेज है, यह संख्या एक जटिल संख्या के रूप में दर्ज की जाती है, बस कोण को निर्दिष्ट करके जैसा कि कैलकुलेटर स्क्रीन पर दिखाया गया है
चरण 5: समीकरण हल करें

अब समीकरण
(वाई * आर) / (एक्स - वाई)
कैलकुलेटर में टाइप किया गया है, यह बिल्कुल वही समीकरण है जिसका उपयोग हम प्रतिरोधी वोल्टेज डिवाइडर को हल करने के लिए करते हैं:)
चरण 6: परिकलित मान


कैलकुलेटर ने परिणाम दिया
१८ + १८७२i
18, प्रतिबाधा का वास्तविक हिस्सा है और इसमें 1MHz पर +1872 का अधिष्ठापन है।
जो प्रारंभ करनेवाला प्रतिबाधा समीकरण के अनुसार 298uH तक काम करता है।
18 ओम उस प्रतिरोध से अधिक है जिसे मल्टीमीटर से मापा जाएगा, ऐसा इसलिए है क्योंकि मल्टीमीटर डीसी पर प्रतिरोध को मापता है। 1 मेगाहर्ट्ज पर त्वचा का प्रभाव होता है, जिसमें कंडक्टर का आंतरिक भाग करंट से बायपास हो जाता है और यह केवल तांबे के बाहर की तरफ बहता है, कंडक्टर के क्रॉस एरिया को प्रभावी ढंग से कम करता है, और इसके प्रतिरोध को बढ़ाता है।
सिफारिश की:
DIY Visuino अनुक्रम घटक का उपयोग करके सर्वो मोटर कोण को कैसे नियंत्रित करें: 10 कदम

DIY Visuino अनुक्रम घटक का उपयोग करके सर्वो मोटर कोण को कैसे नियंत्रित करें: इस ट्यूटोरियल में हम सर्वो मोटर और Arduino UNO, और Visuino का उपयोग अनुक्रम घटक का उपयोग करके सर्वो मोटर कोण को नियंत्रित करने के लिए करेंगे। अनुक्रम घटक उन स्थितियों के लिए एकदम सही है जहां हम अनुक्रम में कई घटनाओं को ट्रिगर करना चाहते हैं। हमारे मामले में सर्वो मोटर degr
गणित-भौतिकी इंद्रधनुष घड़ी: 3 कदम (चित्रों के साथ)
गणित-भौतिकी इंद्रधनुष घड़ी: कुछ समय पहले मेरे पास अपनी खुद की भौतिकी/गणित घड़ी बनाने का विचार था, इसलिए मैंने इसे इंकस्केप में डिजाइन करना शुरू किया। प्रत्येक घंटे, १ से १२ तक, मैंने भौतिकी/गणित सूत्र के साथ प्रतिस्थापित किया: १ - यूलर का समीकरण २ - इंटीग्रल ३ - त्रिकोणमितीय फ़ंक्शन ४ - त्रिकोण का अभिन्न
एलटीस्पाइस का उपयोग करके प्रतिबाधा मापना: 4 कदम
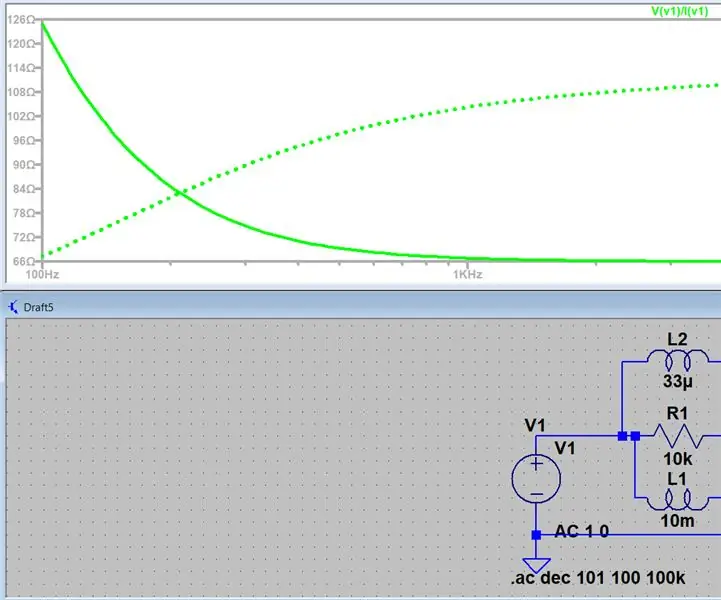
एलटीस्पाइस का उपयोग करके प्रतिबाधा को मापना: सभी को यह एक सर्किट के एसी स्वीप उत्पन्न करने और किसी भी बिंदु पर प्रतिबाधा खोजने के लिए एक सरल परिचय होने जा रहा है, यह मेरे पाठ्यक्रमों में कई बार आया और मेरे लिए कोई भी खोजना बहुत मुश्किल था इसे ऑनलाइन करने का तरीका
त्वरित गणित 2018: 7 कदम
क्विक मैथ 2018: एक ऐसा गेम जो सीखने को फिर से मजेदार बना देता है
लोगों/मनुष्यों/जानवरों/रोबोटों को वास्तव में कूल/उज्ज्वल हीट विजन (आपकी पसंद का रंग) बनाने के लिए जीआईएमपी का उपयोग करने का एक बहुत ही सरल/आसान/जटिल तरीका नहीं है: 4 कदम

लोगों/मनुष्यों/जानवरों/रोबोटों को वास्तव में कूल/उज्ज्वल हीट विजन (आपकी पसंद का रंग) बनाने के लिए GIMP का उपयोग करने का एक बहुत ही सरल/आसान/गैर-जटिल तरीका: पढ़ें…शीर्षक
